What Is The Largest Value A 32bit Register Can Represent As An Unsigned Int? (In Decimal)
A Tutorial on Data Representation
Integers, Floating-bespeak Numbers, and Characters
Number Systems
Man beings use decimal (base 10) and duodecimal (base of operations 12) number systems for counting and measurements (probably because we have ten fingers and 2 big toes). Computers use binary (base 2) number organization, as they are made from binary digital components (known as transistors) operating in two states - on and off. In computing, we besides use hexadecimal (base 16) or octal (base viii) number systems, as a compact class for representing binary numbers.
Decimal (Base 10) Number System
Decimal number arrangement has x symbols: 0, 1, two, 3, 4, 5, 6, 7, 8, and 9, called digits. It uses positional annotation. That is, the least-significant digit (right-most digit) is of the guild of ten^0 (units or ones), the 2nd right-nigh digit is of the club of x^1 (tens), the third right-near digit is of the order of 10^two (hundreds), and and so on, where ^ denotes exponent. For example,
735 = 700 + 30 + 5 = seven×10^two + 3×10^1 + v×10^0
Nosotros shall denote a decimal number with an optional suffix D if ambivalence arises.
Binary (Base 2) Number System
Binary number system has two symbols: 0 and 1, called bits. It is also a positional notation, for instance,
10110B = 10000B + 0000B + 100B + 10B + 0B = 1×2^4 + 0×two^iii + 1×2^ii + one×2^1 + 0×2^0
Nosotros shall denote a binary number with a suffix B. Some programming languages denote binary numbers with prefix 0b or 0B (e.thou., 0b1001000), or prefix b with the bits quoted (e.chiliad., b'10001111').
A binary digit is chosen a bit. Eight bits is called a byte (why eight-bit unit of measurement? Probably because 8=two3 ).
Hexadecimal (Base 16) Number System
Hexadecimal number system uses xvi symbols: 0, 1, 2, iii, iv, 5, 6, 7, eight, 9, A, B, C, D, Eastward, and F, chosen hex digits. It is a positional notation, for example,
A3EH = A00H + 30H + EH = x×16^2 + 3×16^1 + 14×16^0
We shall denote a hexadecimal number (in short, hex) with a suffix H. Some programming languages announce hex numbers with prefix 0x or 0X (e.g., 0x1A3C5F), or prefix ten with hex digits quoted (e.thousand., x'C3A4D98B').
Each hexadecimal digit is as well called a hex digit. Most programming languages have lowercase 'a' to 'f' as well as uppercase 'A' to 'F'.
Computers uses binary system in their internal operations, as they are built from binary digital electronic components with 2 states - on and off. Withal, writing or reading a long sequence of binary bits is cumbersome and error-decumbent (try to read this binary cord: 1011 0011 0100 0011 0001 1101 0001 1000B, which is the same as hexadecimal B343 1D18H). Hexadecimal system is used every bit a meaty form or shorthand for binary $.25. Each hex digit is equivalent to 4 binary bits, i.east., autograph for 4 $.25, every bit follows:
| Hexadecimal | Binary | Decimal |
|---|---|---|
| 0 | 0000 | 0 |
| ane | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | iii |
| 4 | 0100 | 4 |
| 5 | 0101 | five |
| vi | 0110 | 6 |
| seven | 0111 | 7 |
| eight | 1000 | viii |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | thirteen |
| E | 1110 | 14 |
| F | 1111 | xv |
Conversion from Hexadecimal to Binary
Replace each hex digit by the four equivalent bits (as listed in the above table), for examples,
A3C5H = 1010 0011 1100 0101B 102AH = 0001 0000 0010 1010B
Conversion from Binary to Hexadecimal
Starting from the right-most bit (least-significant bit), supplant each group of four bits by the equivalent hex digit (pad the left-about bits with zero if necessary), for examples,
1001001010B = 0010 0100 1010B = 24AH 10001011001011B = 0010 0010 1100 1011B = 22CBH
Information technology is of import to note that hexadecimal number provides a compact form or shorthand for representing binary bits.
Conversion from Base of operations r to Decimal (Base x)
Given a n-digit base r number: dn-1ddue north-2dn-3...d2d1d0 (base r), the decimal equivalent is given by:
dnorthward-1×rnorth-1 + dn-2×rnorthward-two + ... + d1×r1 + d0×r0
For examples,
A1C2H = 10×xvi^3 + 1×16^2 + 12×16^1 + 2 = 41410 (base of operations ten) 10110B = 1×two^4 + one×2^2 + 1×two^1 = 22 (base x)
Conversion from Decimal (Base of operations x) to Base of operations r
Utilise repeated partition/balance. For case,
To convert 261(base 10) to hexadecimal: 261/16 => quotient=16 remainder=5 16/xvi => quotient=1 remainder=0 1/16 => quotient=0 remainder=1 (caliber=0 finish) Hence, 261D = 105H (Collect the hex digits from the residual in reverse order)
The above process is actually applicable to conversion between any 2 base systems. For example,
To convert 1023(base of operations 4) to base 3: 1023(base four)/three => quotient=25D remainder=0 25D/3 => caliber=8D remainder=one 8D/three => quotient=2D residue=2 second/3 => quotient=0 remainder=two (quotient=0 stop) Hence, 1023(base 4) = 2210(base of operations three)
Conversion between Ii Number Systems with Fractional Office
- Separate the integral and the partial parts.
- For the integral function, divide by the target radix repeatably, and collect the ramainder in contrary order.
- For the fractional part, multiply the fractional part by the target radix repeatably, and collect the integral function in the aforementioned order.
Case i: Decimal to Binary
Convert 18.6875D to binary Integral Part = 18D 18/2 => quotient=nine rest=0 9/2 => quotient=4 rest=1 4/2 => caliber=2 remainder=0 2/ii => quotient=1 remainder=0 1/2 => quotient=0 residue=1 (caliber=0 stop) Hence, 18D = 10010B Fractional Part = .6875D .6875*ii=i.375 => whole number is 1 .375*2=0.75 => whole number is 0 .75*2=ane.v => whole number is i .5*2=1.0 => whole number is i Hence .6875D = .1011B Combine, eighteen.6875D = 10010.1011B
Example 2: Decimal to Hexadecimal
Convert 18.6875D to hexadecimal Integral Office = 18D 18/sixteen => quotient=ane remainder=two 1/16 => quotient=0 remainder=1 (quotient=0 terminate) Hence, 18D = 12H Fractional Function = .6875D .6875*16=11.0 => whole number is 11D (BH) Hence .6875D = .BH Combine, xviii.6875D = 12.BH
Exercises (Number Systems Conversion)
- Convert the following decimal numbers into binary and hexadecimal numbers:
-
108 -
4848 -
9000
-
- Convert the post-obit binary numbers into hexadecimal and decimal numbers:
-
1000011000 -
10000000 -
101010101010
-
- Convert the following hexadecimal numbers into binary and decimal numbers:
-
ABCDE -
1234 -
80F
-
- Convert the post-obit decimal numbers into binary equivalent:
-
19.25D -
123.456D
-
Answers: You lot could use the Windows' Calculator (calc.exe) to acquit out number system conversion, by setting it to the Programmer or scientific mode. (Run "calc" ⇒ Select "Settings" carte ⇒ Choose "Programmer" or "Scientific" style.)
-
1101100B,1001011110000B,10001100101000B,6CH,12F0H,2328H. -
218H,80H,AAAH,536D,128D,2730D. -
10101011110011011110B,1001000110100B,100000001111B,703710D,4660D,2063D. - ?? (You work it out!)
Calculator Memory & Information Representation
Computer uses a fixed number of bits to represent a piece of data, which could be a number, a character, or others. A due north-fleck storage location can stand for up to 2^n singled-out entities. For example, a 3-chip retentiveness location tin hold one of these viii binary patterns: 000, 001, 010, 011, 100, 101, 110, or 111. Hence, it can represent at well-nigh 8 singled-out entities. You could utilize them to stand for numbers 0 to seven, numbers 8881 to 8888, characters 'A' to 'H', or up to 8 kinds of fruits like apple tree, orange, banana; or upwardly to 8 kinds of animals like king of beasts, tiger, etc.
Integers, for example, tin can be represented in 8-bit, xvi-fleck, 32-bit or 64-bit. You lot, as the programmer, cull an appropriate flake-length for your integers. Your choice will impose constraint on the range of integers that can be represented. As well the bit-length, an integer tin can exist represented in various representation schemes, eastward.g., unsigned vs. signed integers. An viii-fleck unsigned integer has a range of 0 to 255, while an 8-bit signed integer has a range of -128 to 127 - both representing 256 singled-out numbers.
It is of import to note that a computer memory location merely stores a binary pattern. It is entirely up to you lot, equally the programmer, to determine on how these patterns are to be interpreted. For example, the 8-fleck binary pattern "0100 0001B" tin can be interpreted as an unsigned integer 65, or an ASCII character 'A', or some secret data known simply to you lot. In other words, you have to first decide how to represent a slice of data in a binary blueprint before the binary patterns brand sense. The interpretation of binary pattern is called information representation or encoding. Furthermore, information technology is important that the data representation schemes are agreed-upon by all the parties, i.e., industrial standards demand to be formulated and straightly followed.
One time you decided on the information representation scheme, certain constraints, in particular, the precision and range will be imposed. Hence, it is important to empathise information representation to write correct and loftier-performance programs.
Rosette Stone and the Decipherment of Egyptian Hieroglyphs


Egyptian hieroglyphs (side by side-to-left) were used past the ancient Egyptians since 4000BC. Unfortunately, since 500AD, no 1 could longer read the aboriginal Egyptian hieroglyphs, until the re-discovery of the Rosette Stone in 1799 by Napoleon'due south troop (during Napoleon'southward Egyptian invasion) nearly the boondocks of Rashid (Rosetta) in the Nile Delta.
The Rosetta Stone (left) is inscribed with a decree in 196BC on behalf of King Ptolemy V. The prescript appears in iii scripts: the upper text is Ancient Egyptian hieroglyphs, the heart portion Demotic script, and the everyman Aboriginal Greek. Because information technology presents essentially the same text in all three scripts, and Aboriginal Greek could still exist understood, information technology provided the key to the decipherment of the Egyptian hieroglyphs.
The moral of the story is unless you know the encoding scheme, there is no way that you lot tin decode the data.
Reference and images: Wikipedia.
Integer Representation
Integers are whole numbers or stock-still-signal numbers with the radix point fixed afterwards the least-meaning flake. They are contrast to real numbers or floating-indicate numbers, where the position of the radix signal varies. Information technology is of import to have note that integers and floating-point numbers are treated differently in computers. They have unlike representation and are processed differently (e.thousand., floating-point numbers are processed in a so-called floating-point processor). Floating-point numbers will be discussed later.
Computers use a fixed number of bits to represent an integer. The unremarkably-used scrap-lengths for integers are eight-bit, 16-bit, 32-bit or 64-scrap. Besides bit-lengths, in that location are 2 representation schemes for integers:
- Unsigned Integers: tin can correspond zero and positive integers.
- Signed Integers: can represent zero, positive and negative integers. Three representation schemes had been proposed for signed integers:
- Sign-Magnitude representation
- 1's Complement representation
- two's Complement representation
You lot, equally the programmer, need to decide on the bit-length and representation scheme for your integers, depending on your awarding's requirements. Suppose that y'all need a counter for counting a small quantity from 0 upwardly to 200, y'all might choose the 8-fleck unsigned integer scheme equally there is no negative numbers involved.
north-scrap Unsigned Integers
Unsigned integers tin can represent aught and positive integers, merely not negative integers. The value of an unsigned integer is interpreted as "the magnitude of its underlying binary pattern".
Example 1: Suppose that due north=8 and the binary pattern is 0100 0001B, the value of this unsigned integer is 1×ii^0 + 1×ii^six = 65D.
Example two: Suppose that n=sixteen and the binary pattern is 0001 0000 0000 1000B, the value of this unsigned integer is 1×two^three + 1×2^12 = 4104D.
Instance three: Suppose that n=16 and the binary blueprint is 0000 0000 0000 0000B, the value of this unsigned integer is 0.
An n-bit pattern can correspond 2^north distinct integers. An n-bit unsigned integer can stand for integers from 0 to (2^n)-1, as tabulated beneath:
| north | Minimum | Maximum |
|---|---|---|
| eight | 0 | (2^viii)-1 (=255) |
| 16 | 0 | (2^sixteen)-one (=65,535) |
| 32 | 0 | (2^32)-1 (=4,294,967,295) (nine+ digits) |
| 64 | 0 | (2^64)-1 (=18,446,744,073,709,551,615) (19+ digits) |
Signed Integers
Signed integers can represent nix, positive integers, likewise as negative integers. Three representation schemes are bachelor for signed integers:
- Sign-Magnitude representation
- 1's Complement representation
- 2'southward Complement representation
In all the above three schemes, the most-significant bit (msb) is chosen the sign bit. The sign fleck is used to stand for the sign of the integer - with 0 for positive integers and one for negative integers. The magnitude of the integer, however, is interpreted differently in different schemes.
north-bit Sign Integers in Sign-Magnitude Representation
In sign-magnitude representation:
- The most-meaning bit (msb) is the sign bit, with value of 0 representing positive integer and ane representing negative integer.
- The remaining north-1 $.25 represents the magnitude (absolute value) of the integer. The absolute value of the integer is interpreted as "the magnitude of the (n-1)-scrap binary pattern".
Instance 1: Suppose that n=8 and the binary representation is 0 100 0001B.
Sign fleck is 0 ⇒ positive
Accented value is 100 0001B = 65D
Hence, the integer is +65D
Case two: Suppose that due north=8 and the binary representation is ane 000 0001B.
Sign fleck is 1 ⇒ negative
Accented value is 000 0001B = 1D
Hence, the integer is -1D
Instance three: Suppose that n=8 and the binary representation is 0 000 0000B.
Sign bit is 0 ⇒ positive
Accented value is 000 0000B = 0D
Hence, the integer is +0D
Case 4: Suppose that n=eight and the binary representation is one 000 0000B.
Sign bit is 1 ⇒ negative
Absolute value is 000 0000B = 0D
Hence, the integer is -0D
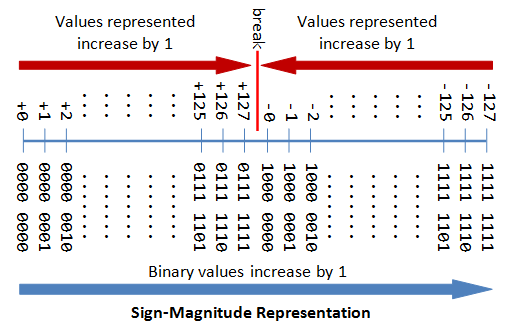
The drawbacks of sign-magnitude representation are:
- There are two representations (
0000 0000Band1000 0000B) for the number nil, which could pb to inefficiency and confusion. - Positive and negative integers demand to be candy separately.
due north-bit Sign Integers in 1's Complement Representation
In 1's complement representation:
- Again, the virtually significant bit (msb) is the sign bit, with value of 0 representing positive integers and 1 representing negative integers.
- The remaining due north-1 $.25 represents the magnitude of the integer, every bit follows:
- for positive integers, the accented value of the integer is equal to "the magnitude of the (north-i)-fleck binary pattern".
- for negative integers, the absolute value of the integer is equal to "the magnitude of the complement (inverse) of the (north-1)-bit binary pattern" (hence called 1'southward complement).
Instance 1: Suppose that northward=8 and the binary representation 0 100 0001B.
Sign bit is 0 ⇒ positive
Accented value is 100 0001B = 65D
Hence, the integer is +65D
Instance 2: Suppose that northward=8 and the binary representation i 000 0001B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 000 0001B, i.e., 111 1110B = 126D
Hence, the integer is -126D
Example iii: Suppose that n=8 and the binary representation 0 000 0000B.
Sign bit is 0 ⇒ positive
Accented value is 000 0000B = 0D
Hence, the integer is +0D
Example 4: Suppose that n=eight and the binary representation i 111 1111B.
Sign bit is ane ⇒ negative
Absolute value is the complement of 111 1111B, i.e., 000 0000B = 0D
Hence, the integer is -0D
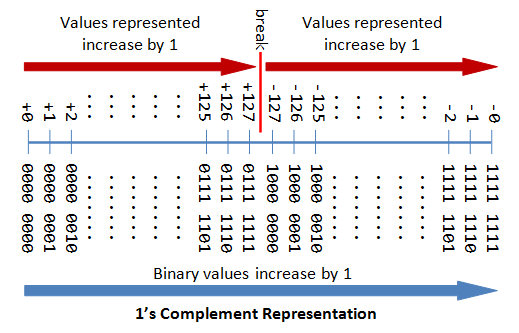
Again, the drawbacks are:
- In that location are two representations (
0000 0000Band1111 1111B) for goose egg. - The positive integers and negative integers need to be processed separately.
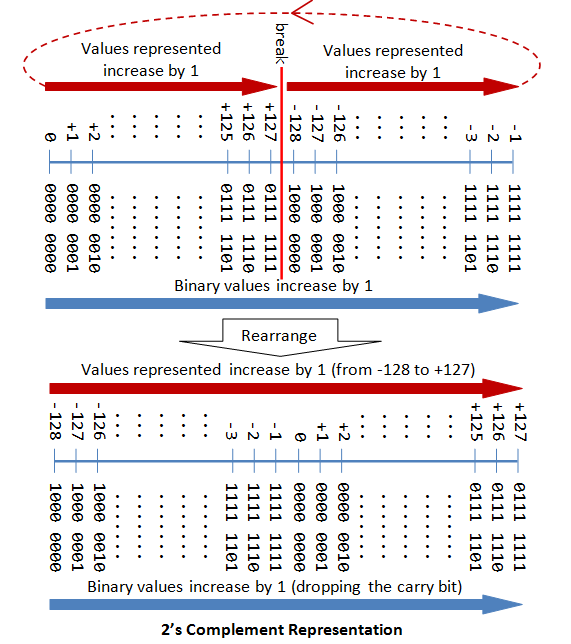
n-fleck Sign Integers in 2'southward Complement Representation
In 2'south complement representation:
- Again, the most significant bit (msb) is the sign bit, with value of 0 representing positive integers and 1 representing negative integers.
- The remaining n-one $.25 represents the magnitude of the integer, every bit follows:
- for positive integers, the accented value of the integer is equal to "the magnitude of the (due north-i)-bit binary pattern".
- for negative integers, the absolute value of the integer is equal to "the magnitude of the complement of the (north-1)-flake binary pattern plus one" (hence called 2'due south complement).
Example 1: Suppose that n=8 and the binary representation 0 100 0001B.
Sign bit is 0 ⇒ positive
Absolute value is 100 0001B = 65D
Hence, the integer is +65D
Example 2: Suppose that n=8 and the binary representation 1 000 0001B.
Sign scrap is 1 ⇒ negative
Absolute value is the complement of 000 0001B plus 1, i.eastward., 111 1110B + 1B = 127D
Hence, the integer is -127D
Example 3: Suppose that n=8 and the binary representation 0 000 0000B.
Sign flake is 0 ⇒ positive
Absolute value is 000 0000B = 0D
Hence, the integer is +0D
Example 4: Suppose that due north=8 and the binary representation 1 111 1111B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 111 1111B plus 1, i.east., 000 0000B + 1B = 1D
Hence, the integer is -1D
Computers utilize 2's Complement Representation for Signed Integers
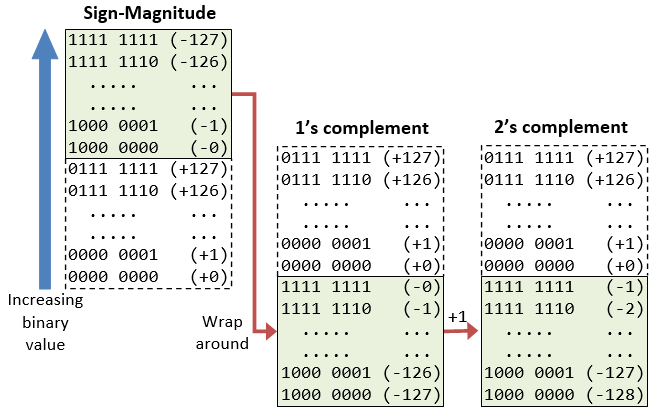
Nosotros have discussed three representations for signed integers: signed-magnitude, one'south complement and 2's complement. Computers utilize 2's complement in representing signed integers. This is because:
- There is only one representation for the number zero in 2's complement, instead of ii representations in sign-magnitude and 1's complement.
- Positive and negative integers can exist treated together in add-on and subtraction. Subtraction can be carried out using the "addition logic".
Instance 1: Addition of Two Positive Integers: Suppose that n=8, 65D + 5D = 70D
65D → 0100 0001B 5D → 0000 0101B(+ 0100 0110B → 70D (OK)
Example 2: Subtraction is treated every bit Improver of a Positive and a Negative Integers: Suppose that n=eight, 5D - 5D = 65D + (-5D) = 60D
65D → 0100 0001B -5D → 1111 1011B(+ 0011 1100B → 60D (discard carry - OK)
Case 3: Addition of Two Negative Integers: Suppose that n=8, -65D - 5D = (-65D) + (-5D) = -70D
-65D → 1011 1111B -5D → 1111 1011B(+ 1011 1010B → -70D (discard behave - OK)
Because of the fixed precision (i.e., fixed number of bits), an n-fleck ii's complement signed integer has a sure range. For example, for north=8, the range of 2'south complement signed integers is -128 to +127. During addition (and subtraction), information technology is important to cheque whether the result exceeds this range, in other words, whether overflow or underflow has occurred.
Example iv: Overflow: Suppose that n=8, 127D + 2nd = 129D (overflow - beyond the range)
127D → 0111 1111B 2D → 0000 0010B(+ 1000 0001B → -127D (wrong)
Example 5: Underflow: Suppose that northward=eight, -125D - 5D = -130D (underflow - below the range)
-125D → 1000 0011B -5D → 1111 1011B(+ 0111 1110B → +126D (incorrect)
The following diagram explains how the 2's complement works. By re-arranging the number line, values from -128 to +127 are represented contiguously by ignoring the carry bit.
Range of n-bit ii's Complement Signed Integers
An n-bit two's complement signed integer tin can stand for integers from -ii^(n-ane) to +2^(n-1)-ane, as tabulated. Take note that the scheme can represent all the integers within the range, without any gap. In other words, at that place is no missing integers inside the supported range.
| n | minimum | maximum |
|---|---|---|
| viii | -(2^7) (=-128) | +(2^7)-1 (=+127) |
| 16 | -(two^15) (=-32,768) | +(2^fifteen)-one (=+32,767) |
| 32 | -(2^31) (=-ii,147,483,648) | +(ii^31)-1 (=+2,147,483,647)(9+ digits) |
| 64 | -(two^63) (=-nine,223,372,036,854,775,808) | +(2^63)-1 (=+nine,223,372,036,854,775,807)(18+ digits) |
Decoding ii'south Complement Numbers
- Check the sign bit (denoted as
South). - If
South=0, the number is positive and its absolute value is the binary value of the remaining n-1 $.25. - If
S=ane, the number is negative. you could "invert the due north-1 bits and plus 1" to become the absolute value of negative number.
Alternatively, you could scan the remaining north-1 bits from the right (least-meaning bit). Await for the first occurrence of 1. Flip all the bits to the left of that beginning occurrence of 1. The flipped pattern gives the absolute value. For example,n = 8, bit pattern = 1 100 0100B South = one → negative Scanning from the correct and flip all the $.25 to the left of the first occurrence of 1 ⇒ 011 one100B = 60D Hence, the value is -60D
Big Endian vs. Trivial Endian
Modern computers store one byte of data in each memory address or location, i.e., byte addressable memory. An 32-bit integer is, therefore, stored in 4 memory addresses.
The term"Endian" refers to the order of storing bytes in computer retentivity. In "Large Endian" scheme, the virtually significant byte is stored offset in the lowest retentiveness address (or big in first), while "Petty Endian" stores the to the lowest degree significant bytes in the everyman retentiveness address.
For example, the 32-flake integer 12345678H (30541989610) is stored as 12H 34H 56H 78H in big endian; and 78H 56H 34H 12H in little endian. An 16-bit integer 00H 01H is interpreted as 0001H in big endian, and 0100H as little endian.
Practise (Integer Representation)
- What are the ranges of 8-bit, 16-bit, 32-bit and 64-bit integer, in "unsigned" and "signed" representation?
- Give the value of
88,0,ane,127, and255in - Give the value of
+88,-88,-1,0,+1,-128, and+127in 8-chip 2's complement signed representation. - Give the value of
+88,-88,-ane,0,+1,-127, and+127in 8-fleck sign-magnitude representation. - Give the value of
+88,-88,-1,0,+1,-127and+127in viii-scrap 1'due south complement representation. - [TODO] more.
Answers
- The range of unsigned n-bit integers is
[0, 2^n - 1]. The range of north-bit 2's complement signed integer is[-ii^(due north-1), +2^(n-one)-1]; -
88 (0101 1000),0 (0000 0000),1 (0000 0001),127 (0111 1111),255 (1111 1111). -
+88 (0101 thousand),-88 (1010 g),-1 (1111 1111),0 (0000 0000),+1 (0000 0001),-128 (yard 0000),+127 (0111 1111). -
+88 (0101 1000),-88 (1101 1000),-i (1000 0001),0 (0000 0000 or 1000 0000),+ane (0000 0001),-127 (1111 1111),+127 (0111 1111). -
+88 (0101 1000),-88 (1010 0111),-1 (1111 1110),0 (0000 0000 or 1111 1111),+1 (0000 0001),-127 (one thousand 0000),+127 (0111 1111).
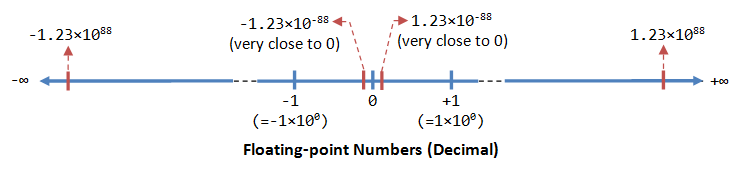
Floating-Point Number Representation
A floating-betoken number (or existent number) can represent a very large (1.23×x^88) or a very small (1.23×10^-88) value. It could besides represent very large negative number (-1.23×x^88) and very small negative number (-i.23×10^88), equally well every bit naught, as illustrated:
A floating-point number is typically expressed in the scientific notation, with a fraction (F), and an exponent (E) of a certain radix (r), in the grade of F×r^Eastward. Decimal numbers employ radix of 10 (F×10^Eastward); while binary numbers apply radix of two (F×2^Due east).
Representation of floating point number is not unique. For case, the number 55.66 can be represented as 5.566×10^1, 0.5566×10^two, 0.05566×10^3, and then on. The fractional part can be normalized. In the normalized form, there is only a unmarried not-zero digit earlier the radix point. For case, decimal number 123.4567 can be normalized every bit 1.234567×ten^2; binary number 1010.1011B tin can be normalized as ane.0101011B×two^3.
Information technology is of import to notation that floating-point numbers suffer from loss of precision when represented with a fixed number of bits (e.yard., 32-bit or 64-bit). This is because there are space number of real numbers (even within a small range of says 0.0 to 0.1). On the other hand, a northward-bit binary pattern can stand for a finite ii^n distinct numbers. Hence, not all the real numbers can be represented. The nearest approximation will be used instead, resulted in loss of accuracy.
Information technology is also important to note that floating number arithmetic is very much less efficient than integer arithmetic. It could be speed up with a so-called defended floating-point co-processor. Hence, use integers if your application does not require floating-point numbers.
In computers, floating-point numbers are represented in scientific notation of fraction (F) and exponent (East) with a radix of 2, in the class of F×2^E. Both Due east and F can be positive as well as negative. Modern computers adopt IEEE 754 standard for representing floating-point numbers. There are two representation schemes: 32-bit single-precision and 64-bit double-precision.
IEEE-754 32-flake Single-Precision Floating-Betoken Numbers
In 32-flake single-precision floating-point representation:
- The nigh significant bit is the sign bit (
Southward), with 0 for positive numbers and 1 for negative numbers. - The following 8 bits represent exponent (
E). - The remaining 23 $.25 represents fraction (
F).
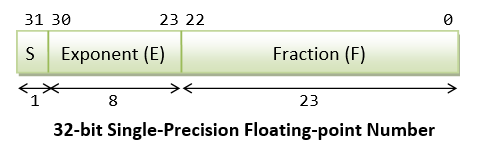
Normalized Form
Let's illustrate with an example, suppose that the 32-bit pattern is 1 1000 0001 011 0000 0000 0000 0000 0000 , with:
-
Due south = one -
E = g 0001 -
F = 011 0000 0000 0000 0000 0000
In the normalized form, the actual fraction is normalized with an implicit leading i in the form of 1.F. In this example, the actual fraction is ane.011 0000 0000 0000 0000 0000 = 1 + 1×ii^-2 + 1×ii^-three = 1.375D.
The sign bit represents the sign of the number, with S=0 for positive and S=ane for negative number. In this example with S=1, this is a negative number, i.due east., -1.375D.
In normalized form, the actual exponent is E-127 (so-chosen excess-127 or bias-127). This is because we need to represent both positive and negative exponent. With an 8-bit E, ranging from 0 to 255, the excess-127 scheme could provide actual exponent of -127 to 128. In this case, E-127=129-127=2D.
Hence, the number represented is -1.375×2^two=-5.5D.
De-Normalized Course
Normalized form has a serious trouble, with an implicit leading 1 for the fraction, it cannot represent the number zero! Convince yourself on this!
De-normalized form was devised to represent zero and other numbers.
For East=0, the numbers are in the de-normalized class. An implicit leading 0 (instead of 1) is used for the fraction; and the actual exponent is always -126. Hence, the number zilch tin can be represented with E=0 and F=0 (because 0.0×ii^-126=0).
We can also represent very small positive and negative numbers in de-normalized form with Eastward=0. For instance, if S=ane, E=0, and F=011 0000 0000 0000 0000 0000. The actual fraction is 0.011=i×2^-two+1×ii^-3=0.375D. Since South=1, it is a negative number. With Due east=0, the actual exponent is -126. Hence the number is -0.375×two^-126 = -4.4×10^-39, which is an extremely small-scale negative number (close to null).
Summary
In summary, the value (N) is calculated as follows:
- For
one ≤ E ≤ 254, North = (-one)^S × 1.F × two^(Due east-127). These numbers are in the so-called normalized course. The sign-bit represents the sign of the number. Fractional part (1.F) are normalized with an implicit leading 1. The exponent is bias (or in excess) of127, so every bit to correspond both positive and negative exponent. The range of exponent is-126to+127. - For
E = 0, N = (-1)^S × 0.F × two^(-126). These numbers are in the so-called denormalized class. The exponent of2^-126evaluates to a very small-scale number. Denormalized form is needed to stand for zero (withF=0andEastward=0). It can also represents very small positive and negative number shut to zero. - For
E = 255, it represents special values, such as±INF(positive and negative infinity) andNaN(not a number). This is beyond the telescopic of this article.
Case 1: Suppose that IEEE-754 32-bit floating-point representation design is 0 10000000 110 0000 0000 0000 0000 0000 .
Sign bit S = 0 ⇒ positive number E = yard 0000B = 128D (in normalized form) Fraction is 1.11B (with an implicit leading 1) = i + i×2^-1 + 1×ii^-2 = 1.75D The number is +one.75 × two^(128-127) = +3.5D
Example 2: Suppose that IEEE-754 32-fleck floating-point representation pattern is one 01111110 100 0000 0000 0000 0000 0000 .
Sign bit S = 1 ⇒ negative number E = 0111 1110B = 126D (in normalized form) Fraction is ane.1B (with an implicit leading 1) = one + 2^-1 = 1.5D The number is -1.5 × 2^(126-127) = -0.75D
Case 3: Suppose that IEEE-754 32-fleck floating-point representation design is 1 01111110 000 0000 0000 0000 0000 0001 .
Sign scrap S = 1 ⇒ negative number E = 0111 1110B = 126D (in normalized form) Fraction is 1.000 0000 0000 0000 0000 0001B (with an implicit leading 1) = 1 + 2^-23 The number is -(1 + 2^-23) × two^(126-127) = -0.500000059604644775390625 (may not be exact in decimal!)
Example 4 (De-Normalized Form): Suppose that IEEE-754 32-fleck floating-point representation pattern is ane 00000000 000 0000 0000 0000 0000 0001 .
Sign flake South = 1 ⇒ negative number Due east = 0 (in de-normalized form) Fraction is 0.000 0000 0000 0000 0000 0001B (with an implicit leading 0) = ane×2^-23 The number is -2^-23 × 2^(-126) = -two×(-149) ≈ -1.4×ten^-45
Exercises (Floating-point Numbers)
- Compute the largest and smallest positive numbers that tin can be represented in the 32-bit normalized class.
- Compute the largest and smallest negative numbers can be represented in the 32-bit normalized form.
- Repeat (i) for the 32-bit denormalized form.
- Repeat (2) for the 32-bit denormalized grade.
Hints:
- Largest positive number:
S=0,East=1111 1110 (254),F=111 1111 1111 1111 1111 1111.
Smallest positive number:Due south=0,Eastward=0000 00001 (one),F=000 0000 0000 0000 0000 0000. - Same equally higher up, but
S=1. - Largest positive number:
Due south=0,Eastward=0,F=111 1111 1111 1111 1111 1111.
Smallest positive number:Southward=0,E=0,F=000 0000 0000 0000 0000 0001. - Aforementioned as above, only
S=1.
Notes For Java Users
You can utilise JDK methods Float.intBitsToFloat(int $.25) or Double.longBitsToDouble(long bits) to create a single-precision 32-bit bladder or double-precision 64-bit double with the specific bit patterns, and print their values. For examples,
Arrangement.out.println(Float.intBitsToFloat(0x7fffff)); System.out.println(Double.longBitsToDouble(0x1fffffffffffffL));
IEEE-754 64-scrap Double-Precision Floating-Betoken Numbers
The representation scheme for 64-flake double-precision is like to the 32-bit single-precision:
- The most pregnant chip is the sign flake (
Southward), with 0 for positive numbers and 1 for negative numbers. - The post-obit xi bits stand for exponent (
E). - The remaining 52 bits represents fraction (
F).

The value (Due north) is calculated equally follows:
- Normalized form: For
ane ≤ E ≤ 2046, N = (-1)^S × one.F × 2^(East-1023). - Denormalized grade: For
Due east = 0, N = (-ane)^S × 0.F × two^(-1022). These are in the denormalized form. - For
East = 2047,Nrepresents special values, such every bit±INF(infinity),NaN(non a number).
More on Floating-Betoken Representation
There are 3 parts in the floating-point representation:
- The sign flake (
S) is self-explanatory (0 for positive numbers and 1 for negative numbers). - For the exponent (
E), a so-called bias (or backlog) is applied so as to correspond both positive and negative exponent. The bias is set at half of the range. For single precision with an eight-chip exponent, the bias is 127 (or excess-127). For double precision with a 11-bit exponent, the bias is 1023 (or backlog-1023). - The fraction (
F) (also called the mantissa or significand) is composed of an implicit leading fleck (earlier the radix betoken) and the partial bits (after the radix betoken). The leading bit for normalized numbers is 1; while the leading chip for denormalized numbers is 0.
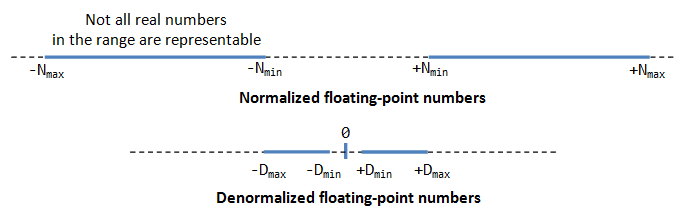
Normalized Floating-Indicate Numbers
In normalized form, the radix point is placed later the kickoff not-zip digit, e,g., nine.8765D×10^-23D, i.001011B×2^11B. For binary number, the leading flake is always 1, and need non be represented explicitly - this saves i bit of storage.
In IEEE 754's normalized grade:
- For single-precision,
1 ≤ E ≤ 254with excess of 127. Hence, the actual exponent is from-126to+127. Negative exponents are used to represent minor numbers (< 1.0); while positive exponents are used to represent big numbers (> one.0).N = (-1)^S × one.F × 2^(Eastward-127) - For double-precision,
one ≤ E ≤ 2046with backlog of 1023. The actual exponent is from-1022to+1023, andDue north = (-1)^S × one.F × 2^(East-1023)
Accept note that n-bit pattern has a finite number of combinations (=2^due north), which could correspond finite distinct numbers. It is not possible to represent the infinite numbers in the real axis (even a small range says 0.0 to 1.0 has infinite numbers). That is, not all floating-indicate numbers tin can be accurately represented. Instead, the closest approximation is used, which leads to loss of accurateness.
The minimum and maximum normalized floating-signal numbers are:
| Precision | Normalized Northward(min) | Normalized N(max) |
|---|---|---|
| Unmarried | 0080 0000H 0 00000001 00000000000000000000000B E = 1, F = 0 N(min) = ane.0B × 2^-126 (≈1.17549435 × 10^-38) | 7F7F FFFFH 0 11111110 00000000000000000000000B E = 254, F = 0 N(max) = i.1...1B × ii^127 = (2 - 2^-23) × ii^127 (≈3.4028235 × ten^38) |
| Double | 0010 0000 0000 0000H N(min) = 1.0B × 2^-1022 (≈2.2250738585072014 × ten^-308) | 7FEF FFFF FFFF FFFFH N(max) = i.i...1B × 2^1023 = (ii - 2^-52) × 2^1023 (≈1.7976931348623157 × 10^308) |
Denormalized Floating-Point Numbers
If E = 0, merely the fraction is not-zippo, then the value is in denormalized class, and a leading bit of 0 is assumed, equally follows:
- For single-precision,
East = 0,N = (-one)^S × 0.F × two^(-126) - For double-precision,
E = 0,Due north = (-one)^Southward × 0.F × ii^(-1022)
Denormalized form can stand for very small numbers airtight to naught, and nada, which cannot be represented in normalized form, as shown in the to a higher place figure.
The minimum and maximum of denormalized floating-point numbers are:
| Precision | Denormalized D(min) | Denormalized D(max) |
|---|---|---|
| Unmarried | 0000 0001H 0 00000000 00000000000000000000001B E = 0, F = 00000000000000000000001B D(min) = 0.0...one × 2^-126 = 1 × ii^-23 × 2^-126 = 2^-149 (≈1.4 × 10^-45) | 007F FFFFH 0 00000000 11111111111111111111111B E = 0, F = 11111111111111111111111B D(max) = 0.1...1 × 2^-126 = (ane-2^-23)×2^-126 (≈1.1754942 × 10^-38) |
| Double | 0000 0000 0000 0001H D(min) = 0.0...1 × 2^-1022 = 1 × 2^-52 × 2^-1022 = 2^-1074 (≈iv.9 × ten^-324) | 001F FFFF FFFF FFFFH D(max) = 0.1...1 × two^-1022 = (1-ii^-52)×2^-1022 (≈4.4501477170144023 × 10^-308) |
Special Values
Zero: Zilch cannot be represented in the normalized form, and must exist represented in denormalized form with E=0 and F=0. In that location are two representations for zero: +0 with S=0 and -0 with Due south=1.
Infinity: The value of +infinity (e.g., i/0) and -infinity (e.g., -one/0) are represented with an exponent of all i'southward (E = 255 for single-precision and E = 2047 for double-precision), F=0, and S=0 (for +INF) and Southward=one (for -INF).
Not a Number (NaN): NaN denotes a value that cannot exist represented as real number (due east.g. 0/0). NaN is represented with Exponent of all 1'southward (E = 255 for single-precision and East = 2047 for double-precision) and any not-naught fraction.
Character Encoding
In computer retention, character are "encoded" (or "represented") using a chosen "character encoding schemes" (aka "character prepare", "charset", "graphic symbol map", or "code page").
For instance, in ASCII (besides as Latin1, Unicode, and many other character sets):
- code numbers
65D (41H)to90D (5AH)represents'A'to'Z', respectively. - code numbers
97D (61H)to122D (7AH)represents'a'to'z', respectively. - code numbers
48D (30H)to57D (39H)represents'0'to'9', respectively.
Information technology is important to note that the representation scheme must exist known before a binary pattern can be interpreted. E.thousand., the 8-flake design "0100 0010B" could represent anything under the sun known simply to the person encoded it.
The most commonly-used character encoding schemes are: 7-chip ASCII (ISO/IEC 646) and 8-bit Latin-x (ISO/IEC 8859-ten) for western european characters, and Unicode (ISO/IEC 10646) for internationalization (i18n).
A 7-chip encoding scheme (such as ASCII) can represent 128 characters and symbols. An 8-chip character encoding scheme (such as Latin-x) tin represent 256 characters and symbols; whereas a xvi-bit encoding scheme (such as Unicode UCS-ii) can represents 65,536 characters and symbols.
7-bit ASCII Lawmaking (aka US-ASCII, ISO/IEC 646, ITU-T T.50)
- ASCII (American Standard Code for Information Interchange) is one of the before character coding schemes.
- ASCII is originally a 7-bit lawmaking. It has been extended to 8-bit to better utilize the 8-flake calculator memory organization. (The 8th-bit was originally used for parity bank check in the early computers.)
- Code numbers
32D (20H)to126D (7EH)are printable (displayable) characters equally tabulated (arranged in hexadecimal and decimal) as follows:Hex 0 1 2 3 4 v half dozen vii 8 nine A B C D E F 2 SP ! " # $ % & ' ( ) * + , - . / 3 0 1 two iii four 5 six 7 eight 9 : ; < = > ? 4 @ A B C D Eastward F Thousand H I J Yard L M N O v P Q R S T U V W X Y Z [ \ ] ^ _ half-dozen ` a b c d e f chiliad h i j yard l g northward o vii p q r s t u 5 w x y z { | } ~
Dec 0 1 2 iii iv 5 six 7 8 9 3 SP ! " # $ % & ' iv ( ) * + , - . / 0 1 v two 3 4 5 6 vii 8 ix : ; 6 < = > ? @ A B C D E seven F Thou H I J Yard L Thousand N O 8 P Q R S T U V Westward X Y 9 Z [ \ ] ^ _ ` a b c ten d e f m h i j k l m 11 n o p q r southward t u five w 12 10 y z { | } ~ - Code number
32D (20H)is the blank or space character. -
'0'to'nine':30H-39H (0011 0001B to 0011 1001B)or(0011 xxxxBwherexxxxis the equivalent integer value) -
'A'to'Z':41H-5AH (0101 0001B to 0101 1010B)or(010x xxxxB).'A'to'Z'are continuous without gap. -
'a'to'z':61H-7AH (0110 0001B to 0111 1010B)or(011x xxxxB).'A'to'Z'are also continuous without gap. However, there is a gap between uppercase and lowercase letters. To convert betwixt upper and lowercase, flip the value of bit-5.
- Code number
- Code numbers
0D (00H)to31D (1FH), and127D (7FH)are special command characters, which are not-printable (non-displayable), as tabulated below. Many of these characters were used in the early days for transmission control (e.m., STX, ETX) and printer control (e.m., Class-Feed), which are now obsolete. The remaining meaningful codes today are:-
09Hfor Tab ('\t'). -
0AHfor Line-Feed or newline (LF or'\north') and0DHfor Carriage-Return (CR or'r'), which are used every bit line delimiter (aka line separator, stop-of-line) for text files. There is unfortunately no standard for line delimiter: Unixes and Mac use0AH(LF or "\n"), Windows employ0D0AH(CR+LF or "\r\due north"). Programming languages such equally C/C++/Java (which was created on Unix) utilize0AH(LF or "\n"). - In programming languages such as C/C++/Coffee, line-feed (
0AH) is denoted as'\due north', carriage-return (0DH) equally'\r', tab (09H) equally'\t'.
-
| Dec | HEX | Meaning | DEC | HEX | Meaning | ||
|---|---|---|---|---|---|---|---|
| 0 | 00 | NUL | Aught | 17 | 11 | DC1 | Device Control ane |
| i | 01 | SOH | Get-go of Heading | 18 | 12 | DC2 | Device Control two |
| 2 | 02 | STX | Outset of Text | xix | 13 | DC3 | Device Command three |
| iii | 03 | ETX | End of Text | 20 | 14 | DC4 | Device Control iv |
| iv | 04 | EOT | Stop of Transmission | 21 | fifteen | NAK | Negative Ack. |
| 5 | 05 | ENQ | Research | 22 | xvi | SYN | Sync. Idle |
| 6 | 06 | ACK | Acknowledgment | 23 | 17 | ETB | End of Transmission |
| 7 | 07 | BEL | Bong | 24 | 18 | CAN | Cancel |
| viii | 08 | BS | Back Space '\b' | 25 | 19 | EM | End of Medium |
| ix | 09 | HT | Horizontal Tab '\t' | 26 | 1A | SUB | Substitute |
| ten | 0A | LF | Line Feed '\n' | 27 | 1B | ESC | Escape |
| eleven | 0B | VT | Vertical Feed | 28 | 1C | IS4 | File Separator |
| 12 | 0C | FF | Form Feed 'f' | 29 | 1D | IS3 | Group Separator |
| thirteen | 0D | CR | Carriage Render '\r' | thirty | 1E | IS2 | Record Separator |
| 14 | 0E | Then | Shift Out | 31 | 1F | IS1 | Unit Separator |
| 15 | 0F | SI | Shift In | ||||
| 16 | ten | DLE | Datalink Escape | 127 | 7F | DEL | Delete |
8-bit Latin-1 (aka ISO/IEC 8859-ane)
ISO/IEC-8859 is a drove of viii-flake character encoding standards for the western languages.
ISO/IEC 8859-one, aka Latin alphabet No. 1, or Latin-i in brusque, is the most commonly-used encoding scheme for western european languages. Information technology has 191 printable characters from the latin script, which covers languages like English language, German language, Italian, Portuguese and Spanish. Latin-1 is backward compatible with the 7-chip US-ASCII lawmaking. That is, the outset 128 characters in Latin-1 (code numbers 0 to 127 (7FH)), is the same every bit US-ASCII. Lawmaking numbers 128 (80H) to 159 (9FH) are non assigned. Lawmaking numbers 160 (A0H) to 255 (FFH) are given as follows:
| Hex | 0 | 1 | 2 | 3 | 4 | v | 6 | 7 | 8 | 9 | A | B | C | D | Eastward | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | NBSP | ¡ | ¢ | £ | ¤ | ¥ | ¦ | § | ¨ | © | ª | « | ¬ | SHY | ® | ¯ |
| B | ° | ± | ² | ³ | ´ | µ | ¶ | · | ¸ | ¹ | º | » | ¼ | ½ | ¾ | ¿ |
| C | À | Á | Â | Ã | Ä | Å | Æ | Ç | È | É | Ê | Ë | Ì | Í | Î | Ï |
| D | Ð | Ñ | Ò | Ó | Ô | Õ | Ö | × | Ø | Ù | Ú | Û | Ü | Ý | Þ | ß |
| Eastward | à | á | â | ã | ä | å | æ | ç | è | é | ê | ë | ì | í | î | ï |
| F | ð | ñ | ò | ó | ô | õ | ö | ÷ | ø | ù | ú | û | ü | ý | þ | ÿ |
ISO/IEC-8859 has 16 parts. Also the most commonly-used Office one, Function two is meant for Cardinal European (Polish, Czech, Hungarian, etc), Part 3 for South European (Turkish, etc), Function 4 for N European (Estonian, Latvian, etc), Role 5 for Cyrillic, Role 6 for Arabic, Part 7 for Greek, Part 8 for Hebrew, Part 9 for Turkish, Function 10 for Nordic, Office xi for Thai, Part 12 was carelessness, Office 13 for Baltic Rim, Part 14 for Celtic, Role 15 for French, Finnish, etc. Office 16 for S-Eastern European.
Other 8-bit Extension of US-ASCII (ASCII Extensions)
Beside the standardized ISO-8859-x, in that location are many 8-bit ASCII extensions, which are not uniform with each others.
ANSI (American National Standards Institute) (aka Windows-1252, or Windows Codepage 1252): for Latin alphabets used in the legacy DOS/Windows systems. It is a superset of ISO-8859-1 with lawmaking numbers 128 (80H) to 159 (9FH) assigned to displayable characters, such every bit "smart" single-quotes and double-quotes. A common problem in web browsers is that all the quotes and apostrophes (produced by "smart quotes" in some Microsoft software) were replaced with question marks or some strange symbols. Information technology it because the document is labeled every bit ISO-8859-1 (instead of Windows-1252), where these code numbers are undefined. Most modernistic browsers and east-mail clients treat charset ISO-8859-1 as Windows-1252 in order to arrange such mis-labeling.
| Hex | 0 | i | 2 | 3 | four | five | 6 | vii | 8 | 9 | A | B | C | D | Eastward | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | € | ‚ | ƒ | „ | … | † | ‡ | ˆ | ‰ | Š | ‹ | Œ | Ž | |||
| 9 | ' | ' | " | " | • | – | — | ™ | š | › | œ | ž | Ÿ |
EBCDIC (Extended Binary Coded Decimal Interchange Code): Used in the early IBM computers.
Unicode (aka ISO/IEC 10646 Universal Character Set)
Earlier Unicode, no single character encoding scheme could represent characters in all languages. For example, western european uses several encoding schemes (in the ISO-8859-x family unit). Even a single language like Chinese has a few encoding schemes (GB2312/GBK, BIG5). Many encoding schemes are in conflict of each other, i.e., the same lawmaking number is assigned to different characters.
Unicode aims to provide a standard graphic symbol encoding scheme, which is universal, efficient, uniform and unambiguous. Unicode standard is maintained by a non-profit organisation called the Unicode Consortium (@ www.unicode.org). Unicode is an ISO/IEC standard 10646.
Unicode is backward compatible with the vii-bit US-ASCII and 8-scrap Latin-1 (ISO-8859-i). That is, the first 128 characters are the same as Us-ASCII; and the commencement 256 characters are the same as Latin-1.
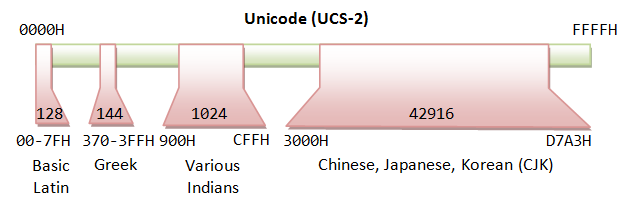
Unicode originally uses 16 bits (called UCS-2 or Unicode Grapheme Set - two byte), which can represent upwardly to 65,536 characters. It has since been expanded to more than 16 bits, currently stands at 21 bits. The range of the legal codes in ISO/IEC 10646 is now from U+0000H to U+10FFFFH (21 bits or almost 2 million characters), covering all current and aboriginal historical scripts. The original 16-bit range of U+0000H to U+FFFFH (65536 characters) is known as Basic Multilingual Plane (BMP), covering all the major languages in use currently. The characters outside BMP are called Supplementary Characters, which are not oft-used.
Unicode has two encoding schemes:
- UCS-two (Universal Character Gear up - ii Byte): Uses two bytes (16 bits), covering 65,536 characters in the BMP. BMP is sufficient for nearly of the applications. UCS-2 is now obsolete.
- UCS-4 (Universal Character Set - 4 Byte): Uses 4 bytes (32 $.25), roofing BMP and the supplementary characters.
UTF-viii (Unicode Transformation Format - eight-bit)
The xvi/32-bit Unicode (UCS-two/four) is grossly inefficient if the document contains mainly ASCII characters, considering each character occupies ii bytes of storage. Variable-length encoding schemes, such as UTF-8, which uses ane-iv bytes to stand for a grapheme, was devised to meliorate the efficiency. In UTF-8, the 128 commonly-used United states-ASCII characters utilize but 1 byte, but some less-commonly characters may crave upward to 4 bytes. Overall, the efficiency improved for document containing mainly United states-ASCII texts.
The transformation between Unicode and UTF-8 is every bit follows:
| $.25 | Unicode | UTF-8 Code | Bytes |
|---|---|---|---|
| 7 | 00000000 0xxxxxxx | 0xxxxxxx | i (ASCII) |
| 11 | 00000yyy yyxxxxxx | 110yyyyy 10xxxxxx | ii |
| 16 | zzzzyyyy yyxxxxxx | 1110zzzz 10yyyyyy 10xxxxxx | 3 |
| 21 | 000uuuuu zzzzyyyy yyxxxxxx | 11110uuu 10uuzzzz 10yyyyyy 10xxxxxx | four |
In UTF-eight, Unicode numbers corresponding to the 7-bit ASCII characters are padded with a leading zero; thus has the same value every bit ASCII. Hence, UTF-8 can be used with all software using ASCII. Unicode numbers of 128 and in a higher place, which are less oftentimes used, are encoded using more than bytes (2-4 bytes). UTF-viii mostly requires less storage and is uniform with ASCII. The drawback of UTF-8 is more than processing ability needed to unpack the code due to its variable length. UTF-8 is the most pop format for Unicode.
Notes:
- UTF-8 uses ane-iii bytes for the characters in BMP (16-bit), and 4 bytes for supplementary characters outside BMP (21-scrap).
- The 128 ASCII characters (bones Latin letters, digits, and punctuation signs) use i byte. Nearly European and Middle Due east characters use a 2-byte sequence, which includes extended Latin letters (with tilde, macron, acute, grave and other accents), Greek, Armenian, Hebrew, Standard arabic, and others. Chinese, Japanese and Korean (CJK) use three-byte sequences.
- All the bytes, except the 128 ASCII characters, take a leading
'1'bit. In other words, the ASCII bytes, with a leading'0'bit, tin can be identified and decoded easily.
Example: 您好 (Unicode: 60A8H 597DH)
Unicode (UCS-2) is 60A8H = 0110 0000 ten 101000B ⇒ UTF-eight is 11100110 10000010 10101000B = E6 82 A8H Unicode (UCS-2) is 597DH = 0101 1001 01 111101B ⇒ UTF-8 is 11100101 10100101 10111101B = E5 A5 BDH
UTF-xvi (Unicode Transformation Format - 16-bit)
UTF-16 is a variable-length Unicode character encoding scheme, which uses 2 to 4 bytes. UTF-16 is not commonly used. The transformation table is as follows:
| Unicode | UTF-xvi Code | Bytes |
|---|---|---|
| xxxxxxxx xxxxxxxx | Aforementioned equally UCS-two - no encoding | 2 |
| 000uuuuu zzzzyyyy yyxxxxxx (uuuuu≠0) | 110110ww wwzzzzyy 110111yy yyxxxxxx (wwww = uuuuu - i) | iv |
Accept note that for the 65536 characters in BMP, the UTF-16 is the aforementioned as UCS-ii (ii bytes). However, 4 bytes are used for the supplementary characters outside the BMP.
For BMP characters, UTF-16 is the same as UCS-ii. For supplementary characters, each grapheme requires a pair 16-bit values, the first from the high-surrogates range, (\uD800-\uDBFF), the second from the low-surrogates range (\uDC00-\uDFFF).
UTF-32 (Unicode Transformation Format - 32-chip)
Same as UCS-4, which uses four bytes for each grapheme - unencoded.
Formats of Multi-Byte (e.g., Unicode) Text Files
Endianess (or byte-order): For a multi-byte character, yous need to take care of the order of the bytes in storage. In big endian, the most meaning byte is stored at the memory location with the lowest address (big byte beginning). In petty endian, the well-nigh significant byte is stored at the memory location with the highest address (little byte offset). For instance, 您 (with Unicode number of 60A8H) is stored as threescore A8 in big endian; and stored equally A8 60 in piffling endian. Big endian, which produces a more readable hex dump, is more commonly-used, and is frequently the default.
BOM (Byte Lodge Mark): BOM is a special Unicode character having lawmaking number of FEFFH, which is used to differentiate big-endian and little-endian. For large-endian, BOM appears as FE FFH in the storage. For little-endian, BOM appears every bit FF FEH. Unicode reserves these two code numbers to forbid it from crashing with another character.
Unicode text files could take on these formats:
- Big Endian: UCS-2BE, UTF-16BE, UTF-32BE.
- Little Endian: UCS-2LE, UTF-16LE, UTF-32LE.
- UTF-xvi with BOM. The first character of the file is a BOM character, which specifies the endianess. For big-endian, BOM appears every bit
Atomic number 26 FFHin the storage. For little-endian, BOM appears asFF FEH.
UTF-8 file is always stored as large endian. BOM plays no function. Withal, in some systems (in particular Windows), a BOM is added as the first character in the UTF-eight file equally the signature to identity the file every bit UTF-8 encoded. The BOM grapheme (FEFFH) is encoded in UTF-8 equally EF BB BF. Adding a BOM as the starting time grapheme of the file is non recommended, equally information technology may be incorrectly interpreted in other arrangement. You tin have a UTF-8 file without BOM.
Formats of Text Files
Line Delimiter or End-Of-Line (EOL): Sometimes, when you utilize the Windows NotePad to open a text file (created in Unix or Mac), all the lines are joined together. This is considering different operating platforms use different character as the then-called line delimiter (or stop-of-line or EOL). Two not-printable control characters are involved: 0AH (Line-Feed or LF) and 0DH (Carriage-Return or CR).
- Windows/DOS uses
OD0AH(CR+LF or "\r\n") as EOL. - Unix and Mac use
0AH(LF or "\n") only.
End-of-File (EOF): [TODO]
Windows' CMD Codepage
Grapheme encoding scheme (charset) in Windows is chosen codepage. In CMD trounce, you lot tin can issue command "chcp" to brandish the current codepage, or "chcp codepage-number" to alter the codepage.
Have notation that:
- The default codepage 437 (used in the original DOS) is an 8-bit character set chosen Extended ASCII, which is different from Latin-i for code numbers above 127.
- Codepage 1252 (Windows-1252), is not exactly the same as Latin-1. Information technology assigns code number 80H to 9FH to letters and punctuation, such every bit smart single-quotes and double-quotes. A common trouble in browser that display quotes and apostrophe in question marks or boxes is because the folio is supposed to be Windows-1252, only mislabelled as ISO-8859-i.
- For internationalization and chinese graphic symbol set: codepage 65001 for UTF8, codepage 1201 for UCS-2BE, codepage 1200 for UCS-2LE, codepage 936 for chinese characters in GB2312, codepage 950 for chinese characters in Big5.
Chinese Character Sets
Unicode supports all languages, including asian languages similar Chinese (both simplified and traditional characters), Japanese and Korean (collectively called CJK). There are more than 20,000 CJK characters in Unicode. Unicode characters are frequently encoded in the UTF-viii scheme, which unfortunately, requires iii bytes for each CJK grapheme, instead of 2 bytes in the unencoded UCS-2 (UTF-sixteen).
Worse still, there are also various chinese character sets, which is not compatible with Unicode:
- GB2312/GBK: for simplified chinese characters. GB2312 uses ii bytes for each chinese character. The most significant bit (MSB) of both bytes are gear up to i to co-exist with 7-bit ASCII with the MSB of 0. There are about 6700 characters. GBK is an extension of GB2312, which include more than characters likewise as traditional chinese characters.
- BIG5: for traditional chinese characters BIG5 too uses 2 bytes for each chinese character. The most significant scrap of both bytes are also set to 1. BIG5 is not compatible with GBK, i.e., the aforementioned code number is assigned to dissimilar graphic symbol.
For example, the earth is made more interesting with these many standards:
| Standard | Characters | Codes | |
|---|---|---|---|
| Simplified | GB2312 | 和谐 | BACD D0B3 |
| UCS-2 | 和谐 | 548C 8C10 | |
| UTF-eight | 和谐 | E5928C E8B090 | |
| Traditional | BIG5 | 和諧 | A94D BFD3 |
| UCS-2 | 和諧 | 548C 8AE7 | |
| UTF-8 | 和諧 | E5928C E8ABA7 |
Notes for Windows' CMD Users: To display the chinese character correctly in CMD vanquish, you need to choose the correct codepage, e.g., 65001 for UTF8, 936 for GB2312/GBK, 950 for Big5, 1201 for UCS-2BE, 1200 for UCS-2LE, 437 for the original DOS. You can utilize control "chcp" to display the current code page and command "chcp codepage_number " to change the codepage. You also accept to choose a font that can display the characters (e.1000., Courier New, Consolas or Lucida Panel, Non Raster font).
Collating Sequences (for Ranking Characters)
A cord consists of a sequence of characters in upper or lower cases, e.k., "apple", "Boy", "Cat". In sorting or comparing strings, if we order the characters co-ordinate to the underlying code numbers (e.g., US-ASCII) character-by-character, the order for the instance would be "Male child", "apple", "Cat" because upper-case letter letters have a smaller code number than lowercase messages. This does non hold with the so-called dictionary order, where the aforementioned uppercase and lowercase letters have the aforementioned rank. Another common problem in ordering strings is "10" (ten) at times is ordered in front of "1" to "9".
Hence, in sorting or comparing of strings, a so-called collating sequence (or collation) is often divers, which specifies the ranks for letters (uppercase, lowercase), numbers, and special symbols. There are many collating sequences available. It is entirely upwards to you lot to cull a collating sequence to meet your awarding's specific requirements. Some case-insensitive dictionary-lodge collating sequences have the same rank for same uppercase and lowercase messages, i.e., 'A', 'a' ⇒ 'B', 'b' ⇒ ... ⇒ 'Z', 'z'. Some example-sensitive dictionary-society collating sequences put the capital letter before its lowercase counterpart, i.east., 'A' ⇒'B' ⇒ 'C'... ⇒ 'a' ⇒ 'b' ⇒ . Typically, space is ranked earlier digits 'c'...'0' to '9', followed by the alphabets.
Collating sequence is often linguistic communication dependent, as different languages utilize different sets of characters (e.g., á, é, a, α) with their ain orders.
For Java Programmers - java.nio.Charset
JDK 1.iv introduced a new coffee.nio.charset package to support encoding/decoding of characters from UCS-two used internally in Java plan to whatsoever supported charset used by external devices.
Case: The following program encodes some Unicode texts in various encoding scheme, and display the Hex codes of the encoded byte sequences.
import java.nio.ByteBuffer; import java.nio.CharBuffer; import coffee.nio.charset.Charset; public class TestCharsetEncodeDecode { public static void main(Cord[] args) { String[] charsetNames = {"Usa-ASCII", "ISO-8859-1", "UTF-8", "UTF-xvi", "UTF-16BE", "UTF-16LE", "GBK", "BIG5"}; Cord message = "Hi,您好!"; System.out.printf("%10s: ", "UCS-2"); for (int i = 0; i < message.length(); i++) { Arrangement.out.printf("%04X ", (int)bulletin.charAt(i)); } System.out.println(); for (Cord charsetName: charsetNames) { Charset charset = Charset.forName(charsetName); Organisation.out.printf("%10s: ", charset.proper noun()); ByteBuffer bb = charset.encode(message); while (bb.hasRemaining()) { System.out.printf("%02X ", bb.become()); } System.out.println(); bb.rewind(); } } } UCS-ii: 0048 0069 002C 60A8 597D 0021 US-ASCII: 48 69 2C 3F 3F 21 ISO-8859-1: 48 69 2C 3F 3F 21 UTF-viii: 48 69 2C E6 82 A8 E5 A5 BD 21 UTF-xvi: Fe FF 00 48 00 69 00 2C sixty A8 59 7D 00 21 UTF-16BE: 00 48 00 69 00 2C 60 A8 59 7D 00 21 UTF-16LE: 48 00 69 00 2C 00 A8 60 7D 59 21 00 GBK: 48 69 2C C4 FA BA C3 21 Big5: 48 69 2C B1 7A A6 6E 21
For Java Programmers - char and Cord
The char data type are based on the original 16-bit Unicode standard called UCS-2. The Unicode has since evolved to 21 $.25, with code range of U+0000 to U+10FFFF. The set of characters from U+0000 to U+FFFF is known as the Basic Multilingual Plane (BMP). Characters higher up U+FFFF are called supplementary characters. A 16-bit Java char cannot hold a supplementary graphic symbol.
Recall that in the UTF-sixteen encoding scheme, a BMP characters uses 2 bytes. It is the same as UCS-ii. A supplementary character uses iv bytes. and requires a pair of 16-bit values, the beginning from the high-surrogates range, (\uD800-\uDBFF), the second from the low-surrogates range (\uDC00-\uDFFF).
In Java, a String is a sequences of Unicode characters. Coffee, in fact, uses UTF-16 for String and StringBuffer. For BMP characters, they are the same as UCS-ii. For supplementary characters, each characters requires a pair of char values.
Java methods that accept a 16-bit char value does not support supplementary characters. Methods that take a 32-bit int value support all Unicode characters (in the lower 21 bits), including supplementary characters.
This is meant to exist an academic word. I have yet to meet the use of supplementary characters!
Displaying Hex Values & Hex Editors
At times, you may demand to display the hex values of a file, especially in dealing with Unicode characters. A Hex Editor is a handy tool that a adept developer should possess in his/her toolbox. There are many freeware/shareware Hex Editor available. Try google "Hex Editor".
I used the followings:
- NotePad++ with Hex Editor Plug-in: Open up-source and free. You lot can toggle between Hex view and Normal view by pushing the "H" push button.
- PSPad: Freeware. Y'all tin can toggle to Hex view past choosing "View" bill of fare and select "Hex Edit Mode".
- TextPad: Shareware without expiration period. To view the Hex value, you need to "open" the file past choosing the file format of "binary" (??).
- UltraEdit: Shareware, non complimentary, 30-24-hour interval trial simply.
Permit me know if you take a better choice, which is fast to launch, easy to employ, can toggle betwixt Hex and normal view, free, ....
The following Java program can exist used to brandish hex lawmaking for Java Primitives (integer, character and floating-point):
1 two 3 4 5 half-dozen 7 8 9 10 eleven 12 13 14 xv 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | public class PrintHexCode { public static void main(String[] args) { int i = 12345; System.out.println("Decimal is " + i); Organization.out.println("Hex is " + Integer.toHexString(i)); Arrangement.out.println("Binary is " + Integer.toBinaryString(i)); System.out.println("Octal is " + Integer.toOctalString(i)); System.out.printf("Hex is %ten\n", i); Arrangement.out.printf("Octal is %o\n", i); char c = 'a'; Arrangement.out.println("Character is " + c); System.out.printf("Character is %c\n", c); Organization.out.printf("Hex is %ten\n", (short)c); System.out.printf("Decimal is %d\n", (brusque)c); float f = 3.5f; Organisation.out.println("Decimal is " + f); Organisation.out.println(Float.toHexString(f)); f = -0.75f; System.out.println("Decimal is " + f); Organization.out.println(Float.toHexString(f)); double d = eleven.22; Arrangement.out.println("Decimal is " + d); System.out.println(Double.toHexString(d)); } } |
In Eclipse, you tin can view the hex code for integer archaic Java variables in debug mode every bit follows: In debug perspective, "Variable" panel ⇒ Select the "menu" (inverted triangle) ⇒ Coffee ⇒ Coffee Preferences... ⇒ Primitive Display Options ⇒ Check "Display hexadecimal values (byte, short, char, int, long)".
Summary - Why Bother about Information Representation?
Integer number 1, floating-point number ane.0 character symbol '1', and string "i" are totally dissimilar inside the computer memory. You need to know the difference to write good and high-performance programs.
- In 8-chip signed integer, integer number
1is represented every bit00000001B. - In 8-bit unsigned integer, integer number
oneis represented equally00000001B. - In 16-flake signed integer, integer number
1is represented equally00000000 00000001B. - In 32-bit signed integer, integer number
aneis represented as000000000000000000000000 00000001B. - In 32-bit floating-point representation, number
1.0is represented every bit0 01111111 0000000 00000000 00000000B, i.due east.,S=0,E=127,F=0. - In 64-bit floating-bespeak representation, number
1.0is represented as0 01111111111 0000 00000000 00000000 00000000 00000000 00000000 00000000B, i.e.,S=0,E=1023,F=0. - In 8-bit Latin-one, the character symbol
'one'is represented equally00110001B(or31H). - In 16-flake UCS-2, the character symbol
'1'is represented as00000000 00110001B. - In UTF-viii, the grapheme symbol
'1'is represented equally00110001B.
If you "add together" a 16-bit signed integer 1 and Latin-one character 'one' or a string "i", y'all could become a surprise.
Exercises (Data Representation)
For the following 16-scrap codes:
0000 0000 0010 1010; 1000 0000 0010 1010;
Requite their values, if they are representing:
- a xvi-bit unsigned integer;
- a xvi-bit signed integer;
- two 8-bit unsigned integers;
- two 8-bit signed integers;
- a xvi-flake Unicode characters;
- ii viii-bit ISO-8859-i characters.
Ans: (1) 42, 32810; (2) 42, -32726; (3) 0, 42; 128, 42; (4) 0, 42; -128, 42; (5) '*'; '耪'; (vi) NUL, '*'; PAD, '*'.
REFERENCES & Resources
- (Floating-Betoken Number Specification) IEEE 754 (1985), "IEEE Standard for Binary Floating-Signal Arithmetic".
- (ASCII Specification) ISO/IEC 646 (1991) (or ITU-T T.50-1992), "Information technology - 7-scrap coded character gear up for information interchange".
- (Latin-I Specification) ISO/IEC 8859-1, "Information technology - viii-scrap single-byte coded graphic character sets - Part 1: Latin alphabet No. 1".
- (Unicode Specification) ISO/IEC 10646, "Information technology - Universal Multiple-Octet Coded Character Set (UCS)".
- Unicode Consortium @ http://world wide web.unicode.org.
What Is The Largest Value A 32bit Register Can Represent As An Unsigned Int? (In Decimal),
Source: https://www3.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html
Posted by: schoenrockbety1981.blogspot.com


0 Response to "What Is The Largest Value A 32bit Register Can Represent As An Unsigned Int? (In Decimal)"
Post a Comment